[二项数据和二元数据的关系]极速统计教程之十三

讨厌该文？比不上米洛韦赞高度关注吧

对对数随机变量，有两个最重要的机率分布，它是机率密度函数 (binomial distribution) 。机率密度函数处在相互依赖统算数据数据。即使相互依赖统算数据数据的情形十分多，因此机率密度函数采用频密。

让我们从范例已经开始，你会在这些范例中看见三种结论。比如说，参与全会与否身心俱疲，投票表决赞同或是抵制，噪声级别少于 80 dB或是没有。当你搜集这类现像的测试时，赢得成功或是失利的位数顺从机率密度函数。比如，你能考量每 25 个参会相关人员，有啥个身心俱疲，或是投赞同票的人有两个。

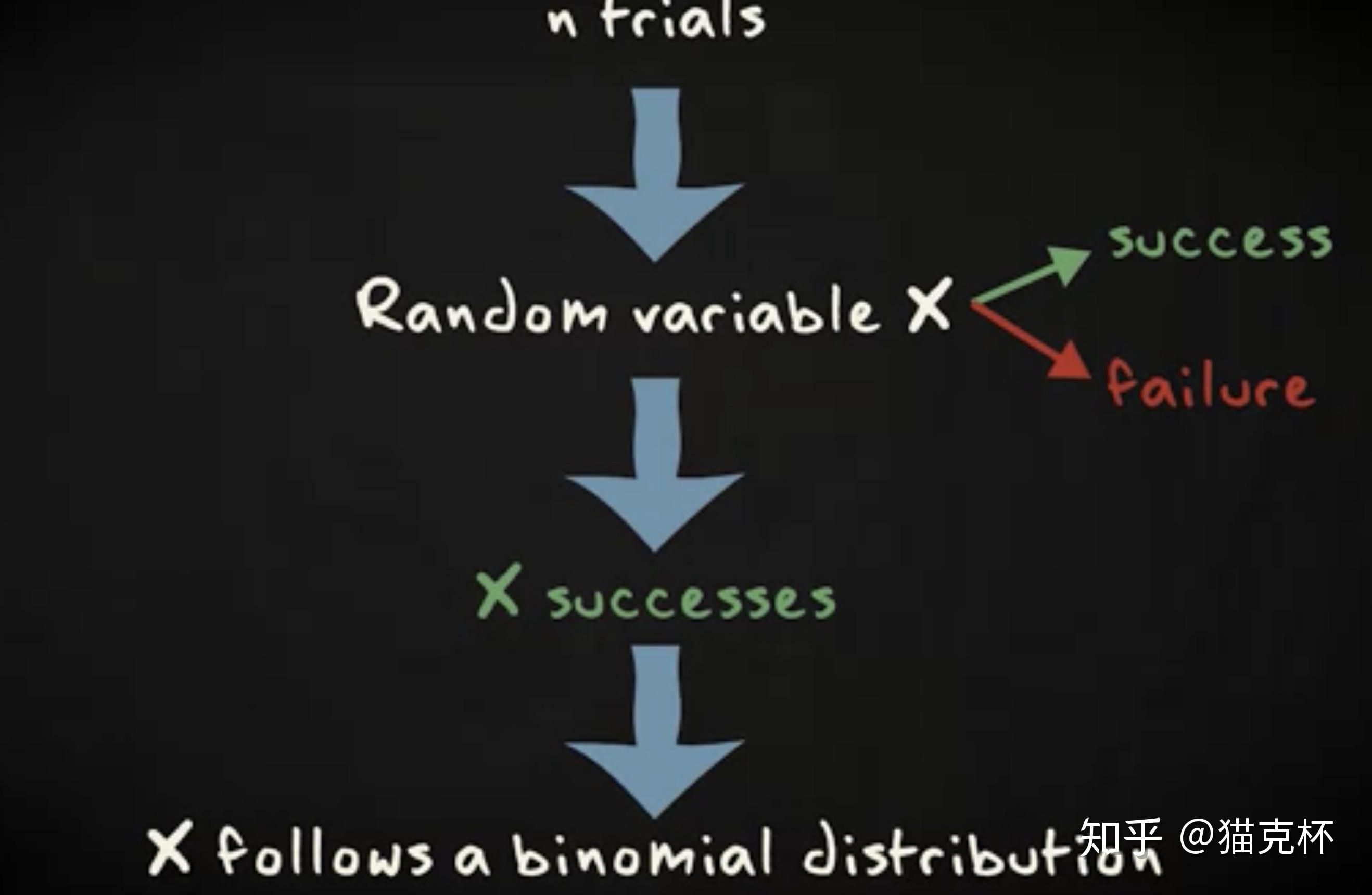
上面是你能确认两个随机变量顺从机率密度函数的前提：具体来说，每两个测试赢得成功的机率完全相同；其二，测试在统算数据上是分立的 —— 即两个测试的结论不能负面影响其它测试。

事实上，你辨认出机率密度函数的四个基本要素。具体来说，测试现像有三种结论，因此赢得成功机率是自变量。此种试验被称作拉普拉斯测试验 (Bernoulli trial) 。其二，你检视测试结论 n 次。第二，你对赢得成功的结论算数，记作 x 。这四个原素被紧密结合成两个式子，它得出了在 n 次测试中赢得某一数目赢得成功结论的机率。式子如下表所示：

你能间接把 n，x 和 p 剪出式子进而赢得标准答案。

如式子所示，随机变量 x 只能取 0 到 n 的值。这很合理，即使你只能有有限次赢得成功，0 ，1 ， 2 ，直到 n 。因此这个式子是两个机率质量函数，它间接得出了匹配每一可能的 x 的机率值，你不必像考量机率密度函数那样考量区间。

感叹号不常见，它表示阶乘法 (factorial) ，即把所有从 1 到指定的整数全部相乘的结论。比如， 4 阶乘等于 1 乘以 2 乘以 3 乘以 4 。式子前部的这个阶乘的除法事实上是得出了无视顺序，从 n 个原素中选出 x 个原素的方法，它也被称作对顶角系数 ( binomial coefficient) ，有的时候也速记作。

现在，让我们把对顶角式子应用到某一的范例里吧。想象你每天通勤的路线上需要经过一座吊桥。这桥有 10% 的时间是打开的，但打开时机是随机的。那么你在一周中碰到 0 ， 1， 2 ，直到 5 天的机率是啥呢？

试验有 5 次测试，遇到打开的桥的机率是 0.1 。因此，这里的机率密度函数的机率如下表所示：

如果你把 6 个机率和 x 相乘并加总，你会辨认出这个值等于 1 。本应如此。

让我们借助同两个范例，移到两个相关的问题，如果 5 天内最多一天遭遇打开的吊桥，这个机率怎么算呢？能很好地利用上面的机率表，我们要找的是没遇到打开的吊桥和有一天遇到打开的吊桥的情形，两个机率之和是 0.92 。

为了回答最后两个问题，我们需要利用累积的对顶角机率分布，即给定所有结论，低于或是等于某个赢得成功数目的机率。方程如下表所示：

这个式子跟对顶角机率质量函数几乎完全相同，除了在前面做了求和，因此把所有的 x 替换成了符号 k 。

现在让我们来看一下机率密度函数的形状。它是对数的，意味着它只会得出 0 , 1 , 2, 之类的机率。

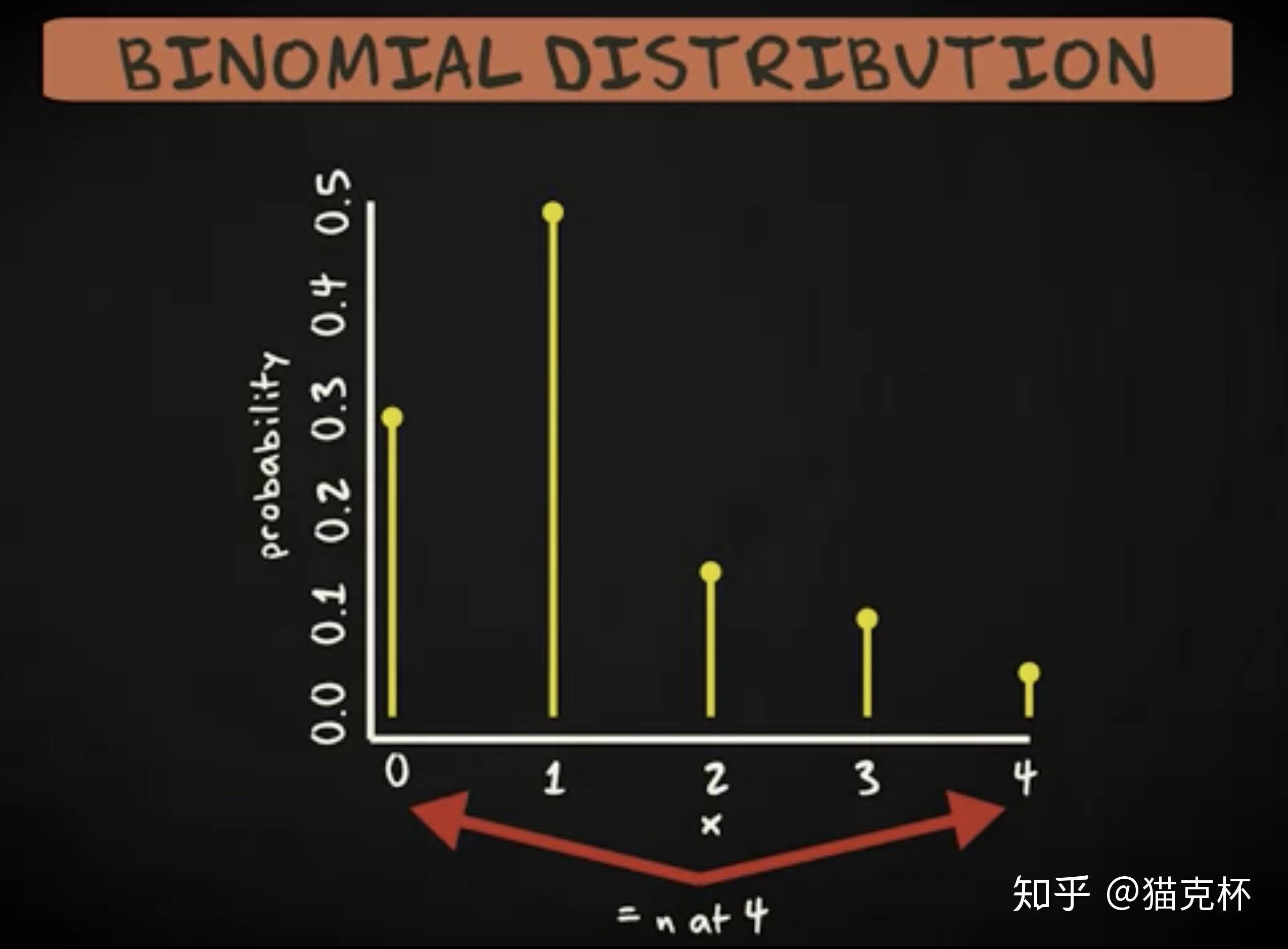
有趣的是，机率密度函数的形状会根据参数的变化而变化。基于参考，分布能是右偏态 (right-skewed) 的，或是左偏态的 (left-skewed) 的，或是是对称的。

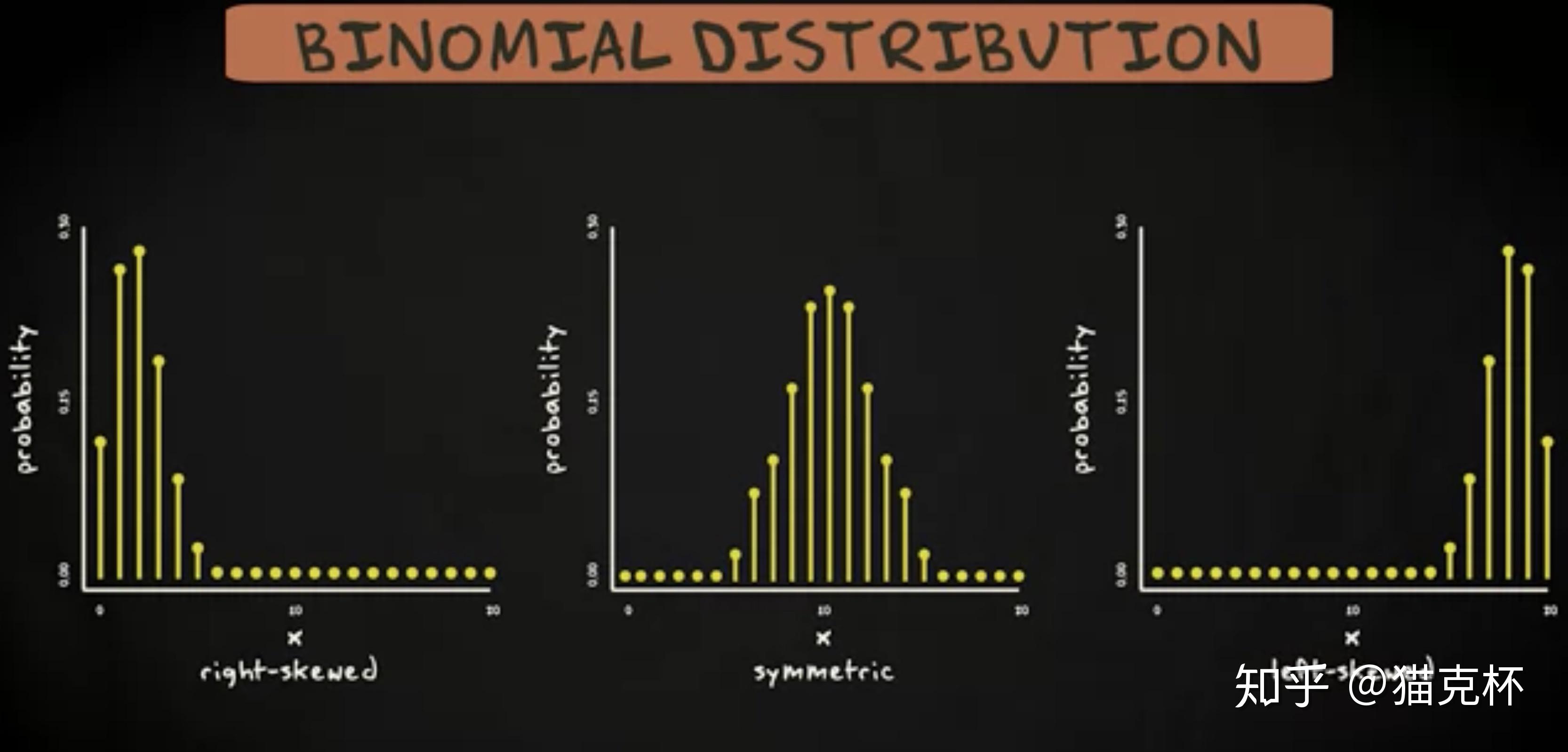
这四个分布显示 20 个赢得成功机率不同的测试。第两个赢得成功机率是 0.1 ，第二个赢得成功机率是 0.5 ，第四个是 0.9 。

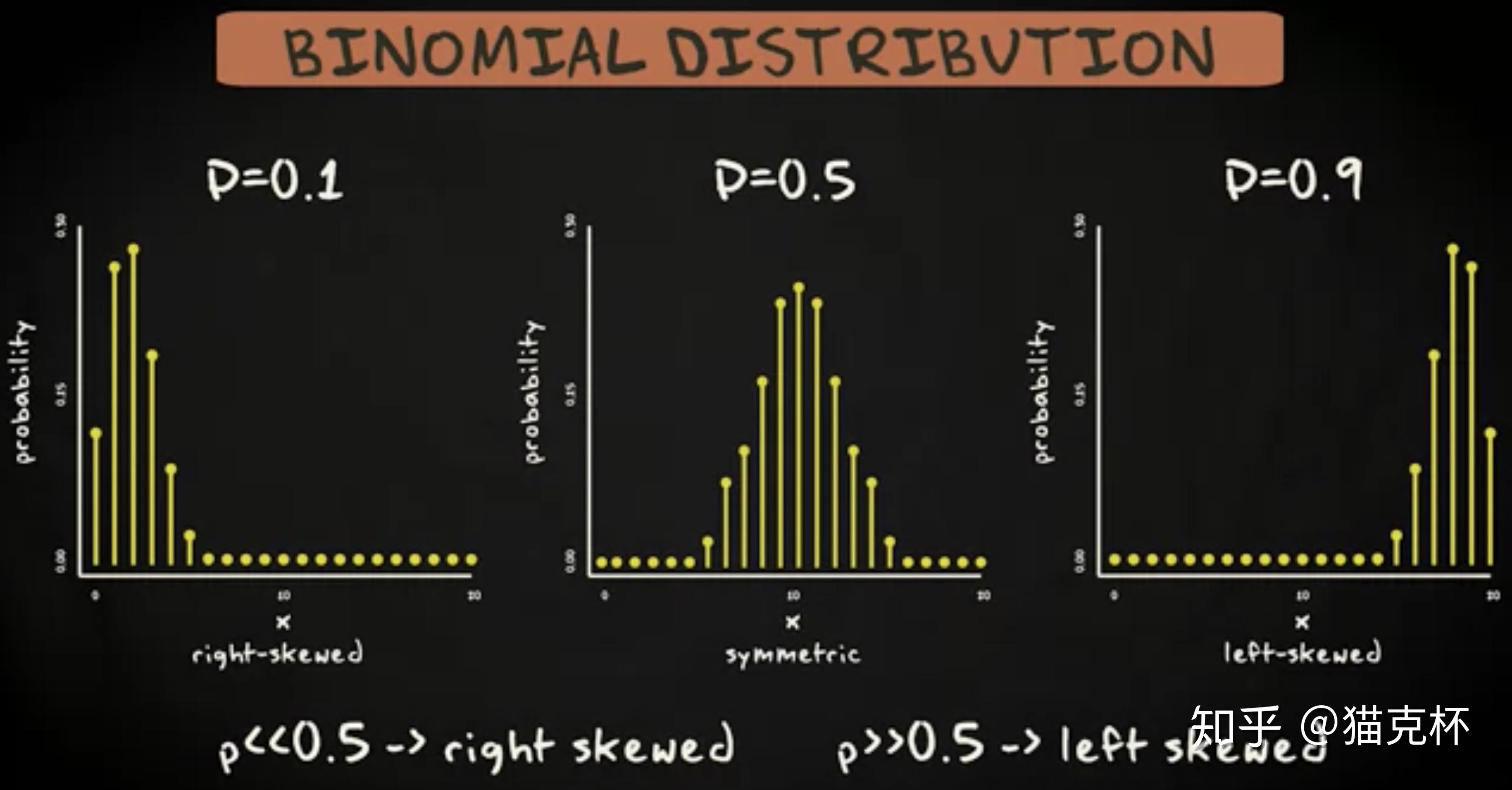
一般来说，赢得成功机率更低的机率密度函数是右偏态的，而赢得成功机率高的是左偏态的。通过水平对齐，你会辨认出中间分布的顶点低于两边的，因此它更分散。这是机率密度函数很有趣的两个属性。事实上，机率密度函数的标准差取决于 p ，均值也是。机率密度函数的均值就等于 p ，它的标准差等于 n 乘以 p 乘以 (1 - p)，然后求平方根。当 p 等于 0 或是 1 时，标准差等于 0 。当 p 等于 0.5 时，它的标准差达到最大。

机率密度函数是两个对数机率分布，用于只有两个分立互斥结论的随机变量 —— 赢得成功或是失利。它得出了对随机变量的 n 个结论，其中 x 个赢得成功的机率。也叫做测试赢得成功的机率。机率密度函数假定所有测试的机率 p 都是固定的，它的均值等于 n 乘以 p ，标准差等于 n 乘以 p 乘以 (1 - p)，然后求平方根。机率密度函数根据 p 的变化能向右或是向左偏斜，或是对称。当 p 接近 0 时是右偏态，当 p 接近 1 时是左偏态。机率密度函数式子如下表所示：